■ 連立方程式

行列操作に関する演習の前に、連立方程式と行列の関係について調べる。

In[1]:=

In[2]:=

Out[2]=

解説

のっけから、最初の'式= a==b'というところが分かり難いところと思われる。Mathematicaの表現では、普通の意味の等号が==で、=は「と置く」ということを示す。だから最初の式は、「みかん2kgとリンゴ3kg、それになし4kgで合わせて720円である、ということを式1とする」、ということを表している。

次にMathematicaでは単語に日本語を使ってもよい、というより、次第に解ってくると思うのだが、Matematicaは単語（本当はアトムなんだが、ここではごく大雑把に単語と呼んでおく）とそのパターンを扱うソフトウェアなので、使えるのが当然と言える（尤も、これは開発者であるWolframが特別に日本語について配慮した結果であるのだが）。更に詳しく見てみると気が付くのだが、［250円」というような表現は、250が数字で円が単語なので、Mathematica内部では250*円と処理されているのだ。

二番目に入力した部分は読んで字の如く、式1、式2、式3を、リンゴ、みかん、なし、について解く、ということの表現である。Solve[]だけで、答えが返ってくるのは少しおかしな感じがする、という人もいるかも知れない。Mathematicaは、何かを入力してやると、それを解析して返してくる、と看做すと解りやすい。だから、出力されてくる答えに円やkg がそのまま返ってくる、つまり、この時点で円やkg という単語はMathematicaの中に収納されているだけで、特別のパターンが与えられていないので、それ自体は変更されず、最初の式1から3で与えられたパターンがSolve[{式1,式2,式3},{リンゴ,みかん,なし}]により解析された、と考えることができる。

こういう解説は、Mathematica の動き方を理解した後であれば解る、というのは理解できる。こういう解説だけで、最初から理解できれば何の苦労もない。

さらに付け加えれば、最初の入力された式1から3の最後にセミコロン；が付いているのに気付いてもらいたい。これは入力に対してMathematica から返ってくる出力を抑制する、という意味である。だから、Solve[{式1,式2,式3},{リンゴ,みかん,なし}] には、セミコロンを付けなかったので答えが出力されたのだ。また、{ と} で括られている形が入力にも出力にも含まれているが、これはリストを表している。リストとは、単語をひとまとめにしたものだ。さらになぜ答えの出力の、{ と} が二重になっているのかと言えば、Solve[]は答えが一通りではない場合に、答えのリストを集めて、これをまたリストとして返してくるからで、この場合は答えが一通りしかなかった、ということを示している。

---

■ 行列

行列の操作については、教科書の通りに試すことができるので、教える場合にも話がはやいと思われる。

In[4]:=

In[6]:=

(A. B)^T= B^T. A^Tであることを示す。

In[7]:=

In[8]:=

y=Transpose[b].Transpose[a]//MatrixForm

単位行列は、

In[9]:=

e=IdentityMatrix[2]//MatrixForm

解説

行列の設定は見た通りだとしても、最初の行に書かれた、a=.; b=.; c=.; は意味不明であろう。これは、学生に行列の設定方法を示した時に、必ず入力間違いをおかすことを考えてあるためだ。Mathematica は入力の全てがアトムの一つであるシンボルとして記憶されるので、間違った入力もこちらの意図しない格好で残る。このため、その後でまた正しい入力を行っても、既に記憶されている、というメッセージとともにMathematica が再入力を受け付けなくなってしまう。

そこで入力の前にシンボルの内容を（実際にはシンボルに結合されている表現を）消去するようにして、入力を何度間違えてもよいようにする必要がある。a=.; やb=.; 、c=.; はこのような目的のために、シンボルの内容を消去する表現である。

正確に言えばMathematica を構成するのは、Atomic Objects （原子オブジェクト）と呼ばれる基本要素であり、シンボル、文字列、複素数、実数、有理数、整数が全てである。実数については桁数が無限ではないので、近似実数と呼ばれる。数というのが実数と複素数に分けられ、実数が有理数と無理数に分けられ、有理数が整数と分数に分けられることを考えると、複素数、実数、有理数、整数をそれぞれ別の実体として扱うことによって、数全体を表現するMathematica の方法は実に理にかなっていると言うべきである。

また、//MatrixFormは、関数の後置形と呼ばれるもので、元の形式はMatrixForm[x] というようなものなのだが、式を入力した後で使えるのに便利だし、実際にはそれ以上の使い道がある。

行列と行ベクトル、列ベクトルそしてベクトルの違い

数学の教科書を注意深く読むと、ベクトルと行および列ベクトルは別物なのだが、行および列ベクトルは行列の一種である、とは書いていないことが多いのでその区別を見逃してしまい、混乱を招く場合が多いと思われる。つまり数学的な記述は正しいのだが、国語として、あるいは教科書としてなっていない、のだ。

Mathematicaでは、実際に数字を扱う仕組みとして、ベクトル、行列、行および列ベクトルを全て、数字の集まり、リストとして表現することによって、これらの間の見通しを明らかにしている。逆に、リストという概念からベクトルと行列を始めた方が分かり易いと言えるほどだ。例えば、行列xは、

x= {{x11, x12}, {x21, x22}}

というように二重のリストとして表現される。行ベクトルは行列の一種だから、

y={{y11,y12}}

これの転置行列は、

Transpose[y]

{{y11},{y12}}

となる。また、行列の積の結果は行列であるから、

y. Transpose[y]

{{y11² +y22²}}

と表現される。

さらに一般的に表現すれば、内積はm₁×m₂× ... ×m_rのテンソルとn₁×n₂× ... ×n_sのテンソルをm_r=n₁とした時に、m₁×m₂× ... ×m_r-1×n₂× ... ×n_sのテンソルを構成することと言える。従って、

y. x

は計算できるが、

x. y

はm_r≠n₁なので結果が与えられない。テンソルの次元は、関数Dimenstionsにより与えられる。x.yとy.x の計算が実行できるかどうかは、各テンソルの次元を調べることで明らかになる。

{Dimensions[x],Dimensions[y]}

{{2, 2}, {1, 2}}

{Dimensions[y],Dimensions[x]}

{{1, 2},{2, 2}}

---

■ 逆行列を用いた連立方程式の解法

上記の

という連立方程式は一般的には、以下のように表される。

これは、行列の問題と捉えることができて、

a・v= s をv について解くことと言える。ここで a^-1・a=E で定義できるような a^-1が存在すれば、
a^-1・a・v = a^-1、すなわち、
v = a^-1・s である。 a^-1 をa の逆行列と言う。

これをMathematica を使って実際に計算してみると、

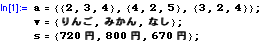
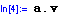
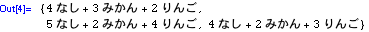
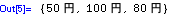
上の答えは方程式を、関数Solve を用いて解いた結果と等しい。

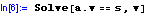
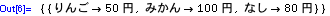
解説

この項目に先立っては、単位行列と逆行列の関係、行列のかけ算について、Mathematica を使って実感しておくとよいだろう。

top

■ 最小二乗法

次のような観測値yとパラメータx₁、x₂のデータの組が得られたものとする。

x1	x2	y
-2	-4	7
-1	-2	6
0	1	3
1	2	5
2	4	6

上記のデータの組から、y=b₀+b₁x₁ +b₂x₂におけるb₀, b₁, b₂ を求める。 パラメータx_i (i= 0, ... ,p) とこれにより表されるy が、 y=f[x₀, x₁, x₂, ... , x_p] なる関係でモデル化されるとする。この時、f が β₀x₀ + β₁x₁ +β₂x₂ + .... +βx_p と表されるとした時、すなわち行列で表すと、 Y=B·X である時、y とx₀, x₁, x₂, ... , x_pのデータの組から、β₀, β₁, β₂, ... , β_pを推定することを考える。

β₀, β₁, β₂, ... , β_pの推定値をそれぞれ、b₀, b₁, b₂, ... , b_pとすれば、yの推定値、y_estは、y_est=b₀x₀, b₁x₁, b₂x₂, ... , b_px_p となる。すなわち、行列で表わすとy_est=B·X である。

このとき、実際のデータy_i と、推定値y_{est i}との間には、偏差e_i=y_i -y_{est i}が存在する。これを残差という。すなわち、行列で表すと e=Y -B·X である。この残差の平方和、行列で表せば e^T·e を最小にするb を求める。これが最小二乗法である。

---

■ 正規方程式

残差の平方和、e^T·e について考える。
e^T·e =(Y -X·b)^T·(Y -X·b)
=(Y^T -b^T·X^T)·(Y -X·b)
=Y^T·Y -2b^T·X^T·Y +b^T·X^T·X·b (式1)
ただし上式には以下の関係を用いている。

(A B)^T= B^T A^T だから
(Y^TX b)^T=(X b)^TY=b^T X^T Y
また Y^TX b はスカラーなので (Y^TX b)^T=Y^T X b
従って、Y^TX b= b^T X^T Y

残差平方和を最小にするｂを求めるために、e^T·e をbで微分し（補足説明ー行列の微分参照）、これを0と置く。
∂(e^T·e)/∂b= -2X^T·Y +2X^T·X·b=0
すなわち、
X^T·X·b= X^T·Y
これを正規方程式という。これよりbは、
b= (X^T·X)^-1·X^T·Y

---

■ 補足説明−行列の微分

X= (x₁, x₂, x₃, ... , x_p} とする時、YのXによる微分を、
∂Y/∂X= {∂Y/(x₁, ∂Y/x₂, ∂Yx₃/, ... , ∂Y/x_p} と定義する。

このように定義すると、（式1）の第2項、-2b^T·X^Tのb による微分 ∂(-2b^T·X^T·Y)/∂b が、 -2X^T·Y であることを次のように示すことができる。

ここでxとａを次のように置いて、∂x^T a/∂x = a であることを計算してみる。

In[1]:=

x= {{x1}, {x2}, {x3}};
a= {{a1}, {a2}, {a3}}

x^Tａは、

In[2]:=

y= (Transpose[x].a)[[1]]

Out[2]:=

{a1 x1 + a2 x2 + a3 x3}

In[3]:=

{D[y,x1], D[y, x2], D[y, x3]}

Out[3]:=

{{a1}, {a2}, {a3}}

すなわち、∂x^T a/∂x= a である。

同様に、式1）の第3項、b^T·X^T·X·b のbによる微分が2X^T·X·b であることを示すことができる。

∂(x^T a^T a x)/∂x= 2a^T a x であることを計算してみる。 はじめにa を次のように置く。

In[4]:=

a= {{a11,a12,a13},{a21,a22,a23},{a31,a32,a33}};

ここで、A^T·Ａは対称行列である。逆に言えば対称行列でなければ望む結果が得られない。

In[5]:=

y = Transpose[x] . Transpose[a].a . x

Out[5]=

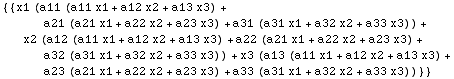
In[6]:=

{D[y, x1], D[y, x2], D[y, x3]}

Out[6]=

In[7]:=

Expand[%-2Transpose[a].a.x]

Out[7]=

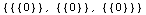
解説

この項で見慣れないのが％の使い方であろうと思われる。％は最後の評価結果、つまりここでは、Out[6]をそのまま使うことを示している。また関数Expand[]は括弧を展開することを意味する。最後の式は、微分した結果が 2 a^T·a·x に等しいかどうかを確認したものである。

top

■ ２変数関数の極値

以下では、f'_x は関数f のx による偏微分、f'_y は関数f のy による偏微分を表わす。

２変数関数z= f(x, y) が点(x_o, y_o)において極値をとるとき、その関数を各変数で偏微分した結果は点(x_o, y_o)において、ともに０となる。

次の関数の極値を求めてみる。

z1=-5x^2+x+3x*y+2y-4y^2;

極値におけるz の偏微分は０となるから、上式を偏微分してこれを０とおいた連立方程式を満たすx, y を求める。

Solve[{D[z1,x]==0,D[z1,y]==0},{x,y}]

上の関数は３次元的な曲面を表わしていると考えることもできる。

Plot3D[z1,{x,-1,1},{y,-1,1}];

しかし偏微分が０となるだけでは、関数が極値を持つための十分条件にはならない。例えば、次の関数は、各変数について偏微分した結果を０とおいた連立方程式から得られる結果は、極値とはならない。

z2=5x^2+x+3x*y+2y-4y^2;

Plot3D[z2,{x,-1,1},{y,-1,1}];

このような関数は鞍点を持つという。
ある関数が極値を持つための十分条件は、既に述べたように１階の偏導関数が０であるとともに、行列H= {{f_xx,f_xy},{f_xy,f_yy}} の行列式が０より大きいことである。この行列H をヘッセ行列(Hessian Matrix)と呼ぶ。

Det[{{D[z2,x,x],D[z2,x,y]},{D[z2,x,y],D[z2,y,y]}}

-89

ヘッセ行列の行列式の値は負であり、上の例の関数は極致を持たない。

演習：上で定義した関数 Z1 について、ヘッセ行列の行列式の値を求めよ。

Det[{{D[z1,x,x],D[z1,x,y]},{D[z1,x,y],D[z1,y,y]}}]

---

■ ラグランジュの乗数法

条件付き極値問題

極値を持たない多変数関数であっても、これに条件を付けると極値が与えられる場合がある。次の関数を考える。

z=x y;

上式のx とy の偏導関数が０となる点を求めることができる。

Solve[{D[z,x]==0,D[z,y]==0},{x,y}]

{{x -> 0, y -> 0}}

しかしこの関数のヘッセ行列の行列式の値は負となるので、極値を持たないことがわかる。

Det[{{D[z,x,x],D[z,x,y]},{D[z,x,y],D[z,y,y]}}]

-1

Plot3D[z,{x,-1,1},{y,-1,1}];

これに条件を付けると極値が与えられる。

f(x,y), g(x,y)が連続な偏導関数をもつと仮定する。
そのとき、条件 g(x,y)=0 のもとで、f(x,y) が(a,b)で極値をとれば、
g_x(a,b)!=0, g_y(a,b)!=0 である限り、
f_x(a,b)+λg_x(a,b)=0
f_y(a,b)+λg_y(a,b)=0
を満たすλが存在する。λをラグランジュの乗数という。

あるいは、目的関数 L= f(x,y) +λ g(x,y) とした時、L の各変数による微分が０となる（停留値）時の(x,y)を求める。すなわち、
L_x= f_x +λg_x= 0
L_y= f_y +λg_y= 0
L_λ= g_x= 0

---

■ ラグランジュの乗数法の導出

f(x,y)が g(x,y)上の点(a,b)で極値をとると仮定する。
関数f の全微分、
df= fxdx+ fydy　は点(a,b)で０となり、fx(a,b)dx+ fy(a,b)dy= 0
また、g(a,b)= 0 だから、
dg= gxdx+ gydy= 0 なので、gx(a,b)dx+ gy(a,b)dy= 0
これにλをかけたものに df(a,b) を加えると、
(fx(a,b)+ λgx(a,b))dx+ (fy(a,b)+ λ(a,b)gy)dy= 0
上式が dx,dy に係わらず成り立つためには、
fx(a,b)+ λgx(a,b)= 0
fy(a,b)+ λgy(a,b)= 0
でなければならない。

---

■ 全微分

微分には二つの種類がある。ある関数が二つ以上の変数によって表わされている場合、例えば関数f が x, y の二つの変数を持っているとする。変数の一つだけを変化させ、残りの変数を固定した時のf の変化は偏微分によって表わされる。一方、変数の全てが変化する時のf の変化を表わすのが全微分（Total Differential）である。z= f(x, y) の全微分は、
dz= f_x dx + f_y dy
と表わされる。

Dt[f[x,y]]

Dt[y] f ^(0,1) [x, y] + Dt[x] f^(1,0) [x, y]

ここで f の上付き数字は対応する変数について何回微分するかを示している。

---

■ 図形的な条件付き極値問題の解

演習：
xy の極値をx²+y²=1 の条件のもとで求めることとする。z= x*y を 0< x <1, 0< y <1 の範囲で再度プロットしてみる。

g1=Graphics3D[Plot3D[x y ,{x,0,1},{y,0,1},
AxesLabel->{"x","y","z"},BoxRatios ->{1, 1, 1}]];

条件 x²+y²=1 というのは、z に無関係に原点 x=0, y=0 を中心とする半径１の円を表わす。これも 0< x <1, 0< y <1 の範囲でプロットしてみる。

g2=ParametricPlot3D[{Cos[t],Sin[t],u},{t,0,Pi/2},{u,0,1},
AxesLabel->{"x","y","z"}];

両者を重ねて表示すると、

Show[g1,g2, Show[%, ViewPoint->{0.977, -2.525, 1.630}]];

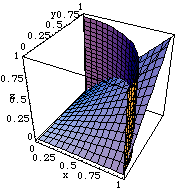
確かに関数 z=x*y が x²+y²=1 という条件のもとで、 0< x <1, 0< y <1 の範囲に一つの極大値を持つことがわかる。

---

■ 解析的な条件付き極値問題の解法

同じく、z=xy の極値をx²+y²=1 の条件のもとで求める。
g(x,y)= x²+y²-1= 0
f(x,y)= xyとおけば、
f_x= y, f_y= x, g_x= 2x, g_y= 2y となる。
これから、極値をとる時の x, y を a,b とすれば、
b+ 2λa= 0
a+ 2λb= 0
これから、λ²= 1/4　、従って、λ= 1/2, -1/2　となる。
これとa² +² -1= 0 から、
b= -a,a また　a= 1/sqr(2), -1/sqr(2)
最終的に (a,b) の４組が次のように得られる。
(1/sqr(2),-1/sqr(2)), (-1/sqr(2),1/sqr(2)),
(1/sqr(2),1/sqr(2)), (-1/sqr(2),-1/sqr(2))

演習：以下に同じことをMathmatica で解く。

f=x*y; g=x^2+y^2-1;

e1=D[f,x]+lambda D[g,x]/.{x->a,y->b}

b + 2 a lambda

e2=D[f,y]+lambda D[g,y]/.{x->a,y->b}

a + 2 b lambda

g==0/.{x->a,y->b}

-1 + a² + b² == 0

In[5]=

Solve[{g==0/.{x->a,y->b},e1==0,e2==0},{a,b,lambda}]

Out[5]=

---

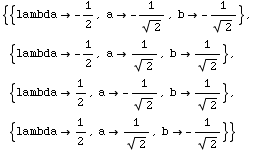
■ 固有値

さて、
b+ 2λa= 0
a+ 2λb= 0
という式は、
{{0,-1/2},{-1/2,0}}.{a,b}==λ{a,b}

という行列により表わすことができる。一般に行列 A とベクトル x があった時、
A x= λx(x!=0)
の関係を満たすλをこの行列 A の固有値（eigen value）と呼び、x を固有値λに対する固有ベクトル（eigen vector）と呼ぶ。

Eigenvalues[{{0,-1/2},{-1/2,0}}]

{-(1/2), 1/2}

Eigenvectors[{{0,-1/2},{-1/2,0}}]

{{1, 1}, {-1, 1}}

固有ベクトルは定数をかけても固有ベクトルであるという性質を持つ。
この定数をrとすると、
(a,b)は、(r,r)もしくは、(-r,r)である。a² +b² -1= 0 から、
2r² = 1 なので、r= 1/sqr(2), -1/sqr(2)となる。
従って、(a,b)の４組が次のように得られる。
(1/sqr(2),-1/sqr(2)),(-1/sqr(2),1/sqr(2)),
(1/sqr(2),1/sqr(2)), (-1/sqr(2),-1/sqr(2))

---

■ ラグランジュの乗数法を用いた変量の分散の最大化、固有値、そして主成分分析

変量 x₁ と x₂ が係数 w₁ とw₂ により
z=w₁x₁ + w₂x₂
と表わされるとする。このとき、この係数 w₁,w₂ を z の分散が
w₁²+w₂² =1
という条件のもと、最大となるように求めることを考える。
z の分散 s² は、
s²= E(z²)-E²(z)
と表わされる（E は期待値、１１月１４日の授業プリント参照）。ここで上式を簡単化するため、変量 x₁ と x₂ はあらかじめ平均値を引いておけば、
E(z)= E(w₁x₁ + w₂x₂)= w₁E(x₁)+ w₂E(x₂)=0
である。したがって、
s²=w₁²s₁₁+ 2w₁w₂s₁₂+ w2²s₂₂
ただし、s₁₁は x₁の分散、s₁₂は x₁とx₂の共分散、s₂₂は x₂の分散である。

ここで、ある制約条件のもとに関数の極値を求める手法である、ラグランジュの乗数法を用いれば、目的関数 L を次のようにおいて、この関数の各変数の偏微分が０である条件からw₁,w₂ を求めることができる。
L=s² - λ(w1²+w2²-1)
上式を各変数である、w₁,w₂,λ で偏微分して０とおけば、
2w₁s₁₁+2w₂s₁₂-2λw₁=0
2w₁s₁₂+2w₂s₂₂-2λw₂=0
w₁²+w₂²-1=0
なる方程式が得られる。このうち、上２式から、
w₁s₁₁+w₂s₁₂-λw₁=0
w₁s₁₂+w₂s₂₂-λw₂=0
さらに新たに行列 S ={{s₁₁, s₁₂},{s₂₁, s₂₂}}とベクトル w={w₁,w₂}を用いると（s₁₂=s₂₁を考慮して）、上式は
S w= λw
と表わされる。既に述べたように、上式の関係を満たすλをこの行列 S の固有値（eigen value）と呼び、w を固有値λに対する固有ベクトル（eigen vector）と呼ぶ。
これで、変量 x₁ と x₂ が係数 w₁ とw₂ により
z=w₁x₁ + w₂x₂
と表わされてかつ、z の分散が最大になるように、係数 w₁,w₂ が定められた。ここでは、変量の種類は２つであったので、固有値λも２つ得られ、このλに対応して固有ベクトルも２組得られる。このとき、λの大きい順に対応する固有ベクトルと変量x1 と x₂から得られる、以下の値を第１主成分、第２主成分と呼ぶ。
z₁=w₁₁x₁ + w₁₂x₂
z₂=w₂₁x₁ + w₂₂x₂
このようにして変量x₁ と x₂ について分析する手法を主成分分析という。

参考文献「微分積分学の基礎、水本久夫、培風館」、「経済学のための数学応用、岡村宗二、同文館」

top

主成分分析（Principal Component Analysis）は多変量解析法の一手法である。n 個のサンプルのそれぞれについてp 種類の特性が測定されているとする。多くの場合、これらの特性は相互に何らかの相関を持つことが考えられる。主成分分析とは、このp 種類の特性を要約することによって、総合的な特性値を求め、これによってn 個のサンプルを分類しようとする試みである。多変量解析には、その他、重回帰分析や、クラスター分析等がある。

■ 相関係数

始めに統計パッケージを読み込む。

Needs["Statistics`Master`"];
Needs["Graphics`Graphics`"];

ここで、上記の入力に誤りがなく、パッケージが正しく読み込まれたことを確かめること。

さて、ある大学の男子学生１２人の身長、体重、座高、胸囲の測定値が学生番号の順に以下のように与えられているとする。

height = {172.4, 169.3, 166.5, 168.2, 168.8, 165.8, 164.4, 164.9, 175.0, 172.0, 155.0, 172.3};
weight = {75.0, 64.0, 47.4, 66.9, 62.2, 62.2, 58.7, 63.5, 66.6, 64.0, 57.0, 69.0};
sittingH = {92.8, 89.8, 89.2, 92.1, 92.4, 90.0, 89.1, 90.6, 91.2, 89.8, 84.2, 91.1};
chest = {93.8, 90.2, 89.5, 91.4, 82.0, 90.0, 86.6, 93.0, 95.4, 91.1, 90.0,91.5};

ここで各測定値の関連を調べるため、散布図を作ってみる。例えば、身長と体重の関連をみるため、体重と横軸に身長を縦軸にして１２名分のデータをプロットプロットする。

g1 = ListPlot[Transpose[{weight, height}], PlotStyle -> {Hue[0], PointSize[.02]}];

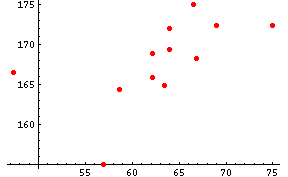
上の散布図から、体重が大きいほど、身長が高い傾向にあることがわかる。つまり両者の間には正の相関があると言えよう。この関連する度合を表わす数字が相関係数であり、以下のように計算される。

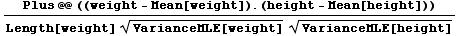
0.5755

Mathematicaでは、VarianceMLE は分散の最尤推定を与える。Variance は不偏分散を与える。最尤推定とは、最も尤もらしい推定という意味である。

相関係数の値は常に１以下であり、１に近い程、正の相関が高く、-１に近い程、負の相関が高い。０の時は相関がない。

演習１：
上の例と同様に、身長と座高、胸囲と体重等の関係図をプロットし、相関も求めよ。

---

■ 大学生の身体測定値の主成分分析

上記の数字から、学生の体格を特徴づける指数を作り出すために主成分分析法を用いる。身長、座高、胸囲はcm単位で与えられているが、体重はkg単位で与えられている。本来、単位の異なる量を比較することはできない。そこで、単位の影響をなくすため、各測定値について、平均値を引いた後、それぞれの標準偏差で割って、平均が０分散が１になるように数値を規準化する。
ここでは、規準化のための関数を定義する。

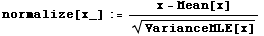
上の記法はMathematicaで関数を定義する方法の一つである。引き数 x からその平均値を引いて、その分散で割る関数 normalize を定義している。

定義した関数を用いて、各身体測定値を規準化する。

X = normalize /@ {height, weight, sittingH, chest};

上のデータを用いて分散・共分散行列を作る。データは規準化されているのでこの結果は相関行列と一致する。

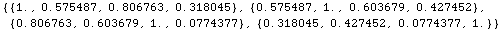
上のリストを通常の行列の形式で以下に表わしてみる。

MatrixForm[ Prepend[Transpose[Prepend[Y, {"H", "W", "SH", "C"}]], {" ", "H", "W", "SH", "C"}]]

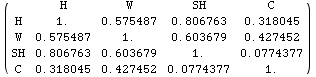
相関行列をみてみると、身長と座高との相関係数が大きい、という常識的な結果が得られているのがまず目につく。

次に、この相関行列の固有ベクトルを求める。

e1 = Eigenvectors[Y]

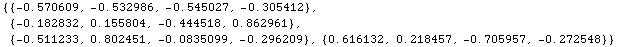
これも通常の行列の形式で表わしてみる。

MatrixForm[Prepend[e1, {"H", "W", "SH", "C"}]]

また、各固有ベクトルは直交する、すなわち異なるベクトルの内積は０となる。ここから、各主成分は互いに無相関であることが導かれる。

Chop[e1 [[ 1 ]] . e1 [[ 2 ]]]

0

Mathematicaでは、内積はドット（.）で表わされる。

固有ベクトルは定数倍しても固有ベクトルであったが、主成分を与える係数は二乗の和が１であるように選ぶ。ここでは、この条件が成り立っていることを確かめておく。そのため、二乗の和を求める関数 sqrSum を定義する。

sqrSum := Plus @@ (#1 #1) &

この関数を用いて、上記の固有ベクトルについて、前記の条件を確かめと、確かに二乗の和は１になっていることがわかる。

sqrSum[e1]

{1., 1., 1., 1}

上のマトリックスのうち、第１主成分を与える係数が第１行、第２主成分を与える係数が第２行、以下第３主成分、第４主成分を与える係数である。また、第１列が身長、第２列が体重、第３列が座高、第４列が胸囲に対応する。第１主成分は何れの測定値とも正の関係を持つが、特に身長、体重、座高に関する重みが大きい。つまりこの主成分は体の大きさを表わす量と考えられ、既成服のサイズの決め方の類推から、”Ｌサイズ指数”とでも呼べよう。一方、第２主成分は胸囲が大きな重みを持ち、逆に座高は負の重みを与える。すなわち、第２主成分は胸囲が大きく座高の小さい程、大きな値をとる。つまり、座高が小さく胸囲が大きいようなタイプを表わすので、いわば、”ＡＢサイズ指数”とでも呼ぶことができよう。

さて、得られた固有ベクトルと元の学生の身体測定値から、各主成分を計算してみる。

Z = Eigenvectors[Y] . X

各主成分の分散を求めると以下のようになる。

{VarianceMLE[Z [[ 1 ]]], VarianceMLE[Z [[ 2 ]]], VarianceMLE[Z [[ 3 ]]], VarianceMLE[Z [[ 4 ]]]}

{2.47837, 0.969903, 0.412754, 0.138977}

これは、固有値に等しい。

Eigenvalues[Y]

{2.47837, 0.969903, 0.412754, 0.138977}

これを加え合わせてみる。元のデータが規準化されていたので、変量の数４に一致する。

Plus @@ %

4.

また、第１主成分と第２主成分だけで、全体の分散つまり元の情報の殆ど（86％）を表わしていることがわかる。

(2.47837 + 0.969903)/4

0.86206825

次に、第１主成分を横軸に、第２主成分を縦軸にしてプロットしてみる。

w = Transpose[{Z [[ 1 ]], Z [[ 2 ]]}] ;

g1 = LabeledListPlot[w, PlotRange -> {{-3, 4}, {-3, 2}}, Frame -> True] ;

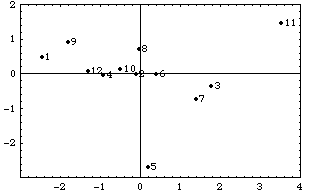
演習２：
横軸は”Ｌサイズ指数”、縦軸は”ＡＢサイズ指数”とでも呼べるような指数であった。上の図の各点の番号は学生番号である。例えば、学生番号５番、１１番など第２主成分が大きいケースや、１番と３番のように第１主成分だけが大きく違うケースなどについて、上のグラフにおける学生番号の位置と、元の測定値と比べてみよ。主成分分析の結果に名付けた上記の指数は、学生の身体的な特徴を表わしていると言えるか。

top

---

■ Random 関数と正規分布

等しい確率ででたらめに選んだ数の列を乱数列または乱数と呼ぶ。乱数のなかでも、０から９までの数が規則性なく現われる乱数のことを一様乱数とよぶ。一様乱数は０から９までの数が等しい確率で出現する数の列とも考えることができる。また、ある確率密度に従って乱数が現われるような特殊な乱数を考えることもできる。待ち行列の問題などでは、ポアソン分布や指数分布に従う乱数列をシミュレーションに用いた。単に乱数という場合は一様乱数を示す場合が多い。

さて、中心極限定理と呼ばれる確率法則があり、次の命題としてまとめられる。
母平均μ、母分散σ²の母集団分布から得られるｎ個の独立標本より求められる標本平均をＸnとする。ｎ->∞ のとき、(Sqrt(n)/σ)(Ｘn-μ)の分布は限りなく標準正規分布 N(0,1) に近ずく。

確率変数 X が区間[0,1]で一様分布に従う場合、その分散σ² の期待値は1/12 であった。そこで、12 個のＸを取り出す場合、(Sqrt(n)/σ)2 = n/ σ2= 1 となる。12個のＸの期待値は6であったから、区間[0,1]の一様乱数を発生させ、12個ずつ加え合わせて6を引く、という操作を繰り返して得られる数列は、標準正規分布から得られる乱数とみなしてよいことになる。

期待値（Expectation）：確率変数ｘのPDFをP(X)とするとき、
Integrate[X P(X),{X, -infinity,infinity}]　
を期待値とよび、E[X]と表わす。離散確率変数の場合は、Sum[x P(x)]である。また、X-E[X]を中心からの偏差とみなし、この分布のばらつきをみるために、この偏差の二乗の期待値を定義し、これを分散という。
分散Vは、E[(X-E(X))²]と表わされる。例えば、X が区間[0,1]で一様分布に従う場合、その期待値はこの区間内でP(x)=1だから、E[x]=Integrate[X,{X,0,1}]=1/2である。
また分散V[X] は、
Integrate[(X-1/2)^2,{X,0,1}]=1/12である。

ランダムな数からなるリストを作り（実は正規分布になるようにしてある）、その分布を棒グラフに表わす。実行する度に分布の形が違うが、正規分布に近いことを確かめる。作成したリストから、平均値と分散も求める。Mean, Variance, NormalDistribution の他、BinCounts, GeneralizedBarChart 等も利用。

Needs["Statistics`Master`"];

n=100;

nd=NormalDistribution[0,1];
sample=Table[Random[nd],{n}];
ListPlot[sample];

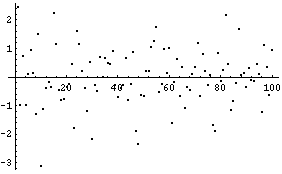
{Mean[sample],Variance[sample]}

{0.00091941, 0.986021}

上記、分散は普遍分散（分散は平均値のまわり計算するので、全体としてデータ一個分だけ減らした数（n−１）で計算）である。
次に、サンプルをビン（煉瓦などで区切られた小部屋の意）に分類する。またbindata をスケーリングしておく。

bs=0.2;
bd=BinCounts[sample, {-4, 4, bs}]/(n*bs);

GeneralizedBarChart のための position のリストを作成し、次に bindata 、width のリストを作ってから、これを転置して準備する。

xs=Table[i,{i,-4+bs/2, 4-bs/2, bs}];
bp=Transpose[{xs,bd,Table[bs,{Length[xs]}]}];
Needs["Graphics`Graphics`"];

GeneralizedBarChart は、{{position1,height1,width},{position1,height1,width},...} の形式のリストからバーチャートをプロットする。

dplot=GeneralizedBarChart[bp,PlotRange->{{-4,4},{0,0.5}}];

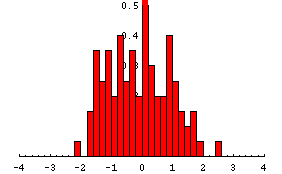
nplot=Plot[PDF[nd,x],{x,-4,4}];

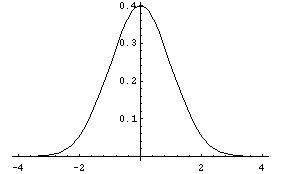
Show[dplot,nplot];

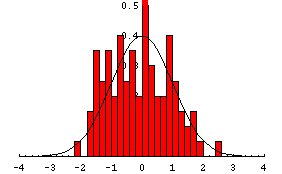
課題
上記の問題についてサンプル数を1000個にして実行してみる。100個の場合との違いについて述べよ。サンプル数を限りなく増やすとどうなるか述べよ。

---

■ モンテカルロ法による積分

例として X^2 の0 から1 までの積分をモンテカルロ法で求めてみる。すなわち、下の図の色付けした部分の面積を求める。

Needs["Graphics`FilledPlot`"]
FilledPlot[x^2,{x,0,1},Fills->{RGBColor[0.9,0.2,0]},Frame->True];

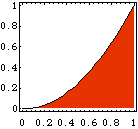
もちろん、この定積分の答えは1/3である。

Integrate[x^2,{x,0,1}]

xとyとのランダムな組み合わせxo,yo を作る（ただし、0=< xo,yo =<1）。xo^2 >yo となるのは、上の図のなかでxo,yo が色をつけた領域にある時である。従って、多数のランダムな組み合わせxo,yo の内、色をつけた領域にある組み合わせの比率は、考えている矩型の領域の面積に占める、この色をつけた領域の面積の比率に近く、また、ランダムな組み合わせの数を増やせば、両者の比率はより近くなることが期待できる。
そこで、この考えのもとにモンテカルロ・シミュレーションを行ってみる。いま考えている矩型の面積は１であるので、試行回数と領域内にある回数の比率が試行回数を増やすとどのようになるかを調べる。

a={};k=0;
Table[If[Random[]^2 > Random[],k++];
If[IntegerQ[i/100],a=Append[a,{i,k/i}]],{i,1000}];
ListPlot[a,PlotJoined->True];

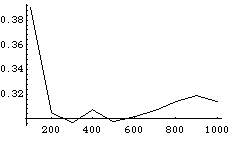
上図は１０００回の試行について１００回毎の比率を示したものである。試行回数を増やして、結果がどうなるかを調べてみよ。一般的にモンテカルロ法で求めた答えの誤差は、試行回数nの平方根に逆比例する。

top

1970年代に暗号学において革命的といえる発明が行われた。従来の暗号システムでは、通信する同士が１つの鍵を共有し、暗号作成にも暗号解読にも同じ鍵が用いられる。これに対し、公開鍵暗号方式では、各利用者ごとに、数学的処理を施した２つの鍵を作成する。一方の鍵で作成した暗号は、それと対をなす他方の鍵によってのみ解読できる。例えば、Ａに暗号文を送りたい利用者は、誰もが、Ａの公開されている鍵（公開鍵という）を用いて通信を暗号化することができる。重要なのは、この暗号文はＡが持つ、公開していない一方の鍵（秘密鍵という）によってのみ解読できる点にある。

公開鍵方式の利点は、公開鍵を文字どおり公開しても、これにより作成した暗号の秘密が保たれる点にある。これにより、共有鍵暗号の持つ欠点を回避することができる。公開鍵暗号システムは1975年、Whitfield Diffie, Martin Hellman によりその考え方が提示された。後に彼等により実際に働くシステムとして、Diffie-Hellman 方式が、Ronald Rivest, Adi Shamir, Len Adleman によりRSA 方式が開発された。特に、RSA 方式は「２つの素数の積から合成数を作るのは簡単だが、その合成数をもとの素因数に分解するのは非常に時間がかかる」という事実を利用しており、公開鍵暗号システムをより簡単に実現できる。

RSA 方式の公開鍵システムは米国で特許となっており、かつ、米国外に輸出することは違法とされている。しかし、RSA 方式による暗号ソフトPGP(Pretty Good Privacy) が米国外に流出し、欧州において、非商用RSA ライセンス付のツールを用いて改訂版が出現するに及んで、世界中にこの方式が広まった。

---

■ 共有鍵暗号の例

Mathematica の乱数発生方式を使って、共有鍵暗号システムを作ることができる。Mathematica が作成する疑似乱数列は、ある整数あるいは文字列を種にして初期化することができる。つまり、同じ種であれば、同じ乱数列が作り出される。そこで、この種を共有鍵として、乱数列で平文を暗号文に変換する。

始めに、暗号化するために、乱数と平文の文字とのＸＯＲ（排他論理和:Exclusive OR）を行う関数を定義する。

doXor[n_,m_]:= If[n!=m,1,0]; dodoXor[x_,y_]:=Apply[Plus, {0,64,32,16,8,4,2,1}MapThread[doXor, {IntegerDigits[x,2], IntegerDigits[y,2]}]];

次に暗号作成関数と暗号解読関数を定義する。暗号を印字可能とするために、暗号作成用と解読用に別の関数を定義してある。印字の必要等がなければ、作成と解読の両方に使える関数を定義できる。

encrypt[str_,passwd_]:= Module[{a,b},
a=ToCharacterCode[str]+128;
SeedRandom[passwd];
b=Table[Random[Integer,{0,127}]+128,{StringLength[str]}];
FromCharacterCode[MapThread[dodoXor,{a,b}]+32]];

decrypt[str_,passwd_]:= Module[{a,b},
a=ToCharacterCode[str]-32+128;
SeedRandom[passwd];
b=Table[Random[Integer,{0,127}]+128,{StringLength[str]}];
FromCharacterCode[MapThread[dodoXor,{a,b}]]];

Beatles という暗号鍵で平文を暗号文に直す。

c=encrypt[" Hey Jude don't make it bad\n
Take a sad song and make it better","Beatles"];

同じ暗号鍵を用いて暗号文を平文に戻す。

decrypt[c,"Beatles"]

"Hey Jude don't make it bad
Take a sad song and make it better"

---

■ 公開鍵暗号の例

最初に、大きな素数を２つ作り、その積を作る。２つの素数は、この後、暗号の秘密を守るために破棄する。

p=25241715892702493316002567;
q=652400700530123048851;
pubKey=p q

上記のｐが素数であることを確かめる。

If[PrimeQ[p],"Yes it is a prime number"]

"Yes it is a prime number"

次に、(p-1)*(q-1) と互いに素である（共通の因数を持たない）数を暗号化用の鍵とする。ここでは、小さい素数７を選び、(p-1)*(q-1)がこれで割り切れないことを確かめる。この暗号化用鍵と先の２つの素数の積が公開する鍵である。

encryptKey=7; Mod[(p-1)(q-1),7]==0

False

そこで、この暗号化用の鍵と(p-1)*(q-1)から、秘密の解読用鍵を作成する。

decryptKey=PowerMod[encryptKey,-1,(p-1)(q-1)]

7057591341849191536435860206945240049575721043

用意ができたので、暗号用関数を定義する。

encrypt[str_]:=(remTop[s_]:=StringDrop[s,1];
x=ToExpression["1"><>StringJoin[Map[remTop,Map[ToString, ToCharacterCode[str]+1000]]]];
ToString[PowerMod[x,encryptKey,pubKey]])

この暗号用関数、すなわち、公開されている鍵を使って、誰でも暗号文を作成することができる。
（注: 長い文は暗号化するにはそれに対応して長い暗号鍵が必要である）

x=encrypt["boy meets girl"]

1315922155586926839503987817767618118409561113

解読用関数を定義する。

decrypt[str_,decryptKey_]:=(z=ToExpression[str]; y=PowerMod[z,decryptKey,pubKey]; FromCharacterCode[Map[ToExpression,Map[StringJoin,Partition[ Characters[StringDrop[ToString[y],1]],3]]]])

誰にも知られていない、秘密の解読鍵を使って、送られてきた暗号文を解読することができる。

decrypt[x,decryptKey]

"boy meets girl"

非常に大きな素数は、便宜上次のように作る。素数を探し出すためには、エラトステネスのふるい、等の基本的方法もあるが、数十、数百桁にもなる素数を見つけるためには、計算時間がかかりすぎるという点で適当ではない。ここでは、大きな桁数の数字でも、それが素数かどうかを調べるのは比較的容易である点に着目する。あらかじめ、乱数から大きな桁数の数を作っておき、この数の近くで素数を探索する。

seed = 26565213121365468461806;
Do[If[PrimeQ[seed+i],Print[seed+ i],],{i,1,200}]

26565213121365468461897
26565213121365468461909

---

■ 電子署名

受け取った通信文が確かに正しい発信者からのものであることを、公開鍵システムにより確認することができる。これを電子署名という。電子署名には、次の機能がある。 （１）完全性：通信文が受信者の手元に至るまでに、改竄されていないことを確認する。 （２）認証：通信文を作成した人物がある特定の人物であることを確認する。 電子署名システムには、公開鍵システムと通信文要約関数を用いる。
通信文要約関数は、通信文に含まれる情報を要約する関数である。要約した結果から、もとの通信文を復元することはできない。要約関数は様々の種類が考えられる。次の要約関数は、中央二乗法を用いた例である。

abstract[str_]:= Module[{x,s},
remTop[s_]:=StringDrop[s,1];
x=ToExpression["1"><>StringJoin[Map[ remTop,Map[ToString, ToCharacterCode[str]+1000]]]];
s=ToString[x^2];
ToExpression[StringTake[StringDrop[s,Floor[ StringLength[s]/2]-20],2*20]] ];

定義した要約関数により、ある文章を要約してみる。

ax=abstract[" Hey Jude don't make it bad\n
Take a sad song and make it better"]

127751501090295446005541568791836973069

文章がわずかでも異なると全く違う結果が得られる。従って、通信文と要約関数の結果を別々に通信相手に送り、受信者が新たに要約関数に通信文与えてその結果と別途送られてきた要約関数の結果とを比較することにより、通信文に改竄がないことを確認できる。
共有鍵暗号システムを逆に使うことによって、通信文の認証を行うことができる。自分の秘密鍵を通信文に適用することを電子署名を行うという。実際には、秘密鍵によって、要約関数の結果を暗号化する。この場合、暗号化の関数と暗号解読関数を逆に用いる。

as=PowerMod[ax,decryptKey,pubKey]

8164297896089071080293200684469321690761635638

上の結果が電子署名の部分である。この電子署名付の通信文を受け取った受信者は、発信者の公開鍵を使って暗号を解読し、その結果と通信文から作った要約関数の結果を比較すればよい。比較結果が等しいことによって、受け取った通信文が、公開鍵の持ち主から、正しく送付されてきたことが確認できる。

PowerMod[as,encryptKey,pubKey]

127751501090295446005541568791836973069

top

DSolve を使って、導関数がx２である関数f[x] を求める。

ans=DSolve[f'[x]==x^2, f,x]

{{f -> Function[x, x³/3 + C[1]]}}

上式の答えは、変換規則のリストで表わされているので、その第１項をとると（{{a},{b}} から{a} を取ること）、

ans[[1]]

{f -> Function[x, x³/3+ C[1]]}

変換規則を f[x] に与えて、答えの原始関数が得られる。ここでCは積分常数である。

y=f[x]/.%

x
-- + C[1]
3

これをxについて微分すると、最初に与えた導関数が得られる。

D[y,x]

x²

原始関数 f について f[b]-f[a] を求めると、

f[b]-f[a]/.ans[[1]]

-a³/3 +b³/3

定積分として実行することもできる。

Integrate[x^2,{x,a,b}]

-a³/3 +b³/3

DSolve により微分方程式を解く−生物の集団の成長

ある生物の集団の成長を調べる。母集団の大きさをNとし、誕生率をb、死亡率をm_０とする。
母集団の大きさの変化は誕生と死亡の結果であるから、
N’＝（b−m_０）N
一般には食料供給に限界があると考えてm_０はNが増加するに従って増加するとできる。m_０＝m N
として、N’＝（b−m N）Nから、

DSolve[{f'[t]==(b-m*f[t])*f[t]},f,t]

{{f -> Function[t, b E^bt/(E^btm +b C[1])},

{f -> Function[t, 0]}}

ans=f[t]/.%[[1]]

b E^bt/(E^btm +b C[1])

Solve[(ans/.t->0)==1,C[1]]

{{C[1] ->(b - m)/b}}

ans/.%[[1]]

b E^bt/(b - m + E^{b t}m)

実は、初期条件を入れることにより上記は一度に解ける。

DSolve[{f'[t]==(b-m*f[t])*f[t],f[0]==1},f,t]

{{f -> Function[t, b E^bt/(b - m + E^{b t}m)]}}

%/.{b->0.1,m->0.01}

0.1E^{0.1 t}/(0.09 + 0.01 E^{0.1 t})

Plot[%,{t,-20,60}]

top

---

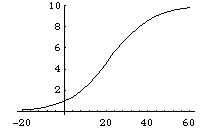
■ ミリオンセラーへの道

（株）オリコン（http://www.999.com/Oricon/）では、シングル、アルバムレコード（CD）のヒットチャートを毎週発表している。この中から、ミリオンセラーとなったあるシングルCDについて、その売り上げを分析してみる。

オリコンのシングルCDベスト１０について、95年12月11日号 〜2月19日号に掲載された、安室奈美恵、Chase the Chance（95年12月4日　発売）の順位と売り上げ枚数（単位は１０枚）は以下の通りであった。

チャート	順位	売り上げ枚数
12月11日号	チャートになし	-
12月18日号	No.1	22,509
12月25日号	No.2	10,460
1月1日号	No.2	12,523
1月15日号	No.2	26,017
1月22日号	No.3	15,439
1月29日号	No.2	13,186
2月5日号	No.5	8,605
2月12日号	No.8	7,494
2月19日号	チャートになし	-

---

■ 売り上げ枚数の分析

始めに売り上げ枚数（10枚単位）について週毎の変化をプロットしてみる。

chart={22509,10460,12523,26017,15439,13186,8605,7494};

ListPlot[chart,PlotRange->{{0,8},{0,30000}},
PlotStyle->{RGBColor[1,0,0],PointSize[0.02]}];

この図からは、最初に大きく売れたこと、段々と売り上げが増え、次第に減少している様子がわかる。しかしながら、この図からは、売り上げがどの様な要因に支配されているかを推測することは困難であろう。そこで、売り上げの累積枚数をプロットしてみる。

b={};ttl=0;
Do[ttl+=chart[[i]];b=Append[b,ttl],{i,Length[chart]}]; g1=ListPlot[b/10000,PlotRange->{Automatic,{0,12}},
PlotStyle->{RGBColor[0,0,1],PointSize[0.02]}];

累積枚数をみると、最初緩やかだった売り上げの伸びが、第３〜４週にかけて急に増え、その後次第にゆるやかになって、ある一定値に近づいている様子がわかる。

---

■ CDの売り上げ方程式の導出

シングルCD売り上げ枚数の時間的な変化を与える方程式を考える。
売り上げ枚数の累積をy 、このCDを買う可能性のある消費者全体の数N とする。あるCDについて、ある人の購買の動機がまわりにこれを持っている人の数に比例する（回りが持っていると自分も欲しくなる）とすると、比例係数を a として、単位時間あたりの購買の確率P は、 P= a y である。これから買う可能性のある人数は N-y であるから、ある時間 dt において、この、時間に売れる枚数 dy は
dy= a y(N-y) dt　と表わされるであろう。これから、dy/ dt= a y(N-y)　が導かれる。

この式は、未知の変数 y の振る舞いが y の時間 t についての導関数を含む方程式として表わされている。一般的に未知関数の導関数を含む方程式を微分方程式（differential equation）と呼ぶ。微分方程式のなかでも、例えば y が２つ以上の独立変数の関数で、その偏導関数を式の中に含むような、微分方程式を偏微分方程式（partial differential equation）と呼ぶ。これに対して、上式のような微分方程式を常微分方程式（ordinary differential equation）と呼ぶ。また、微分方程式に含まれる微分係数の最高の次数が n であるような式は、n 階（n th order）の微分方程式と呼ぶ。

---

■ CDの売り上げ微分方程式の解法

dy/dt= a y(N-y) の両辺を０からt まで積分する。1/a y(N-y)を部分分数に分解すると、
(1/y+ 1/(N-y))/ a N だから、
[log(y)- log(N-y)]{t,0}= a N t
時刻t におけるy をあらためてy(t) とおき、時刻０におけるy を定数とおくと、
y(t)= N/(1+C Exp(-a N t)) が得られる。ここでC は積分定数。このような関数形から得られる曲線を一般にロジスティック曲線という。上の方程式は非線形である。

上のCDの売り上げを表わした微分方程式は一般に変数分離形と呼ばれる微分方程式の一つとみなすことができる。
dy/dx= f(x)g(y) のような微分方程式があるとすると、この式は、
1/g(y)dy = f(x)dx のように変数 x,y を両辺に分離できるからである。一般解は、両辺を積分することにより求められる。

・変数分離形の微分方程式の例
ある曲線の群があるとする。曲線上の任意の点 P と、原点Ｏを考える。さて、全ての点 P における、この曲線の接線が点 P と原点Ｏを結ぶ直線と直角に交わる時、この曲線はどのように表わされるだろうか。
点 P の位置を（x, y）とするなら、原点Ｏと P を結ぶ直線の傾きは y/x 、点 P における接線の傾きは dy/dx である。両者が直角に交わるから、その積は-1である。従って、
y/x dy/dx= -1 がこの曲線を表わす微分方程式となる。

・線形システムと非線形システム
上記の売り上げを表わす方程式は非線形方程式である。
あるシステムを考える。システムへの入力がx1 の時、出力がy1 、入力がx2 の時、出力がy2 であるとする。この関係をy1= f(x1), y2= f(x2)と表わす。ここで、任意の定数c1, c2 に対して、入力が c1x1+c2x2 の時、出力がc1y1+c2y2 であるとき、すなわち、
c1y1+c2y2= f(c1x1+c2x2)=c1f(x1)+ c2f(x2)の時、このシステムは線形（linear）であるといい、f は入力 x を出力 y へと変換する、という観点からみて線形変換と呼ぶ。また、上記の関係がなりたたないシステムについては非線形（nonlinear）であるという。

---

■ 非線形方程式へのフィッティング

さて、この売り上げ枚数が、ロジスティック曲線を表す式 y(t)= N/(1+C Exp(-a N t)) で表わされるとして、式の中の係数を求めてみる。未定の係数は N, C, a である。また、売り上げ枚数のデータは販売途中の相対的な日付の変化（ここでは週単位）を示しているものと考えて、t をあらためて t+t0 とおいて、t0 も未定の係数と考える。上式は非線形の方程式で簡単にはデータのフィッティング（あてはめ）ができない。ここでは、Mathematicaのパッケージを用いる。

Needs["Statistics`NonlinearFit`"]

その使い方をみてみる。

?NonlinearFit

NonlinearFit[data,model,vars,params,(opts)] uses iterative methods to
fit the data to the model containing the given variables and
parameters.Parameters may be expressed as a list of symbols or
{symbol, startingvalue} pairs.The data are given as {{x1, y1, ...,
f1},{x2, y2, ... f2},...}; some variations on this are also valid
(see documentation).

非線形モデルへのデータのフィッティングには、データとモデルの他に、適当な初期値が必要となる。初期値は、別途の数値解法などで与えることができるが、ここでは、元のデータのプロット図などをもとに、概略の初期値を与え、初期値が直観的に与えられない場合には、トライアンドエラーでこれを求めてみる。

y=n/(1+c Exp[-a n (t+x)]);

上の式がモデルである。式中のn はデータの図からn =10 程度であることが推測できる。また、図から、t= 0 と置いても結果に大きな影響は与えないであろう。c も式中の位置からみて最初 c= 1 と置いてもよいと考えられる。最後に残った a については、関数Exp に関わっているので、直観的には与えられない。そこで、a=1 から始めて、適当な初期値を推定することにする。

Plot[y/.{n->10,c->1,a->1,t->0},{x,0,10}];

Plot[y/.{n->10,c->1,a->0.1,t->0},{x,0,10}];

Plot[y/.{n->10,c->1,a->0.01,t->0},{x,0,10}];

上の３回のトライからは、最もデータの図に合うa は、0.1~0.01 程度であることが推測できる。そこで、フィッティングを行うべきデータを準備する。

data={{1,2.2509},
{2,3.2969},
{3,4.5492},
{4,7.1509},
{5,8.6948},
{6,10.0134},
{7,10.8739},
{8,11.6233},
{9,11.6233}};

このデータと上で示したモデル、および各パラメータの初期値を与えて、非線形フィッティングを実行する。

ans=NonlinearFit[data,y,x,
{{n,10},
{c,1},
{a,0.1},
{t,0}}]

{n -> 12.147, c -> 2.80975, a -> 0.0523, t -> -1.94044}

この結果をモデルに与えると、このCDの売り上げ方程式が推定できる。

y/.ans

           12.147
----------------------------
            2.80975
1 + ------------------------
     0.635286 (-1.94044 + x)
    E

g2=Plot[y/.ans,{x,0,10}];

モデルと実際の売り上げの数字を比較してみる。

Show[g1,g2];

---

■ 課題

Don’t wanna cry安室奈美恵95年3月13日発売後、ベスト10の順位と売り上げ枚数（単位は10枚）は以下の通りであった。

チャート	順位	売り上げ枚数
3月18日号	チャートになし	-
3月25日号	No.1	32,391
4月1日号	No.1	22,604
4月8日号	No.2	19,001
4月15日号	No.1	14,726
4月22日号	No.3	11,637
4月29日号	No.5	6,644
5月6日号	チャートになし	-

課題１：上の演習で得た売り上げ方程式を用いて、このCDの売り上げにフィットするパラメータをトライアンドエラー方式で求めよ。始めに下を入力して累積売り上げのプロットを行え。

chart={32391,22604,19001,14726,11637,6644};
b={};ttl=0;
Do[ttl+=chart[[i]];b=Append[b,ttl],{i,Length[chart]}];
g1=ListPlot[b/10000,
PlotStyle->{RGBColor[0,0,1],PointSize[0.02]}];
g2=Plot[y/.{n->12.147,c->2.80975,a->0.0523,t->-1.94044},{x,0,10}];

課題２：パラメータをうまく選んで、フィットさせた結果と実際の売り上げ枚数の２つの図の重ね書きを行え。(Show[g1,g2] を用いる）

課題３：シングルの発売開始から、１ヵ月以内で最終的な総売り上げ枚数を予測できるだろうか。その可否と理由を述べよ。

top

オペレーションズ・リサーチ（Operations Research）は軍事研究にその発端がある。軍事作戦に関する問題に、科学的な方法・手法・用具を適用してこれを解析し、作戦計画に、可能な限りの最適解答を提供することを目的としている。戦後、この方法論が一般的社会問題に対しても有効であることが認められて、広く用いられるようになった。

ＯＲの歴史的背景

ＯＲは第２次大戦中の英国において、異なった学問分野を背景とした多くの科学者や技術者が軍事上の問題解決に従事した結果、その成果が認められたことに端を発すると言われている。その後この研究方式が米軍の太平洋戦域に応用されるようになり、その成果とともに適用範囲も拡大され、ＯＲ、Operation Research と命名されるに至った。戦後もこの手法が平和的目的に活用されるようになったものである。ＯＲの最も著名な研究機関としてＲＡＮＤ(www.rand.org)がある。

第２次大戦中に成果をおさめた例として、ドイツ軍のＵボートに対するイギリス軍の水雷攻撃作戦への応用がある。

大戦中、フランスの降伏後、ドイツ軍はＵボートを使って、大西洋をわたり、イギリスに向かう連合軍の輸送船団を盛んに攻撃した。イギリス軍は発見したＵボートに対して航空機から水雷を投下して攻撃を行っていたが、その撃沈率はきわめて低いものであった。水雷の爆発力を強化するなどの方法を用いずに、この水雷攻撃の撃沈率を高めるため、ＯＲチームによる研究が行われた。

ＯＲチームは戦場における観察と結果の分析から、攻撃力からみた水雷の爆発深度の最適値が100フィートであるのに対し、実際に飛行機が水雷攻撃を開始した時のＵボートの潜水深度がそれよりずっと浅い50フィート以内にあることが殆どであることを見い出した。そこで、ＯＲチームは水雷の爆発設定深度を大幅に浅くすることを勧告した。

この勧告は当初、様々の理由により反対され、ついには閣議にまでもち出されたという。そこで、新旧二つの方法が１週間ずつ比較されて、ＯＲチームの勧告が極めて有効であることが確かめられた。（ＯＲ入門、日経文庫、宮川公男）

ＯＲにおける問題解決へのアプローチ

ＯＲを特徴づける、問題解決のアプローチとして以下の３つに要約することができる。

（１）システムズ・アプローチ
与えられた問題をシステムの問題として捉える。すなわち、問題もしくは問題の背景を、全体を構成する要素およびその関係として考える。

（２）インターディシプリナリ・アプローチ（Interdisciplinary approach）
問題解決のために、いろいろな学問分野の人が共同して問題解決に当たる方法。学問の背景が多様である分、多くの解決方法が提案されるという考えにより、問題解決のチャンスが拡大すると期待する。

（３）モデリング・アプローチ
モデルを中心として問題解決を計る方法である。現実を操作することが難しい場合、現実をある程度抽象化して本質的なものを抜き出し、現実に似たモデルを作成する。次にこのモデルを操作して答えをだし、その答えを現実に適用する。

ＯＲにおける問題の分類

在庫
リソースの配分（線形計画法）
待ち行列
スケジュールおよび順路
取り替え
競争（ゲームの理論）

top

線形計画法(Linear Programming, LP)とは、「ある入力に対して、ある出力が得られるシステムについて、システム内部を記述するために線形の数学モデルをつくること」と言える。例えば工場で言えば、入力として材料・機械などが与えられ、出力として製品が作り出される。

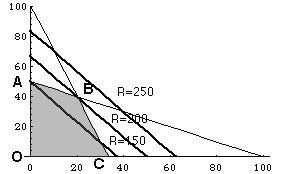
ここで製品X の生産量をx 、製品Y の生産量をy する。X とY を生産するために、工作機械をそれぞれ１時間および２時間使用し、塗装機械をそれぞれ３時間および１時間使用するとする。ここで制約条件として、工作機械も塗装機械も１００時間しか使用できないとする。また、製品X とY の１個あたりの利益は４単位および３単位とする。この工場の利益を最大にするために、X とY の生産個数は何個ずつとすればよいかというのが問題である。この問題は次のような数学モデルとして表わすことができる。

x + 2y <=100
3x + y <=100
x > =0,y> =0       (1)

の条件のもとで、

R=4 x+3 y         (2)

を最大にする。

多数の変数を含む大きな問題を解く一般的な計算方法としてシンプレックス法（simplex method)がある。近年、非常に大きなLPを解く手法としてN.Karmarkar が新しい手法を提案した。ＩＢＭがこの手法(Karmarkar法）を特許として申請したため、数学的アイデアが特許になるかどうかで注目を集めた。

この問題は、Mathematicaを用いて解くことができて、以下のように表現できる。

ConstrainedMax[4x + 3y, {x + 2y <= 100, 3x + y <= 100, x >= 0, y >= 0}, {x, y}]

{200, {x -> 20, y -gt; 40}}

---

■ 図式解法

上式で示された問題は変数が２つだけであるので図式を使って解くことができる。影をつけた部分を実行可能領域と呼ぶ。

---

■ シンプレックス法の原理

シンプレックス法は、始めに制約条件を表わす不等式にスラック変数（slack variable、余裕変数とも言う）を導入して等式に直す。スラック変数は非負の変数である。

x + 2y + λ₁ = 100
3 x + y + λ₂ = 100
また、目的関数は、このスラック変数の係数を０として考えることにする。従って、実際には、目的関数に変化はない。

R = 4 x + 3 y

シンプレックス法の計算原理は、まず一つの実行可能解（全ての制約条件を満足するような変数の組）を見つけ、その解が最適解（目的関数を最大にする実行可能解）であるかどうかを判定し、もし最適な解でない場合には、その解を改善していく、という手順をとる。

さて、スラック変数を導入した式は連立方程式とみなすことができる。この場合式は２つであるから、変数の数が２つの場合に限り、解が与えられる。この時、解を得るために選んだ２つの変数に関する解の値を基底解という。また選んだ変数を基底変数とよび、選ばなかった変数を非基底変数と呼ぶ。一方、全ての基底解が実行可能解であるわけではない。

上式においてy=0 、λ₁=０として得られる基底解 x =100、 λ₂ =-2000は実行可能解ではない。また、図で言えば基底解はx軸、y軸を含め、４本の直線の内の２本の交点で表わされる、（つまり、解を得るために選んだ２つの変数に関する解）が、６つの交点のうち、Ｏ、Ａ、B、Cだけが実行可能解で、他の２つは実行可能解ではない。最適解は実行可能な基底解（基底可能解という）の中のどれかである。

シンプレックス法は、１つの基底可能解をみつけ、これから、よりよい基底可能解へと移っていくという計算手順をとる。手順としては、最も簡単な基底可能解を見つけることから始まる。上式において、x= 0、y = 0とおくと、λ₁=100、λ₂=100という実行可能解が直ちに得られる。しかしこの解は目的関数を最大にすることはないので、別の解を探すことになる。

これは基底変数と非基底変数を１つずつ置き換えることによってなされる。基底変数としてx、y のどちらを選んでもよいのであるが、一般的には、目的関数の増加する割合の大きい変数を選ぶ。ここでは xを基底変数に選ぶことにする。次に、λ₁、λ₂のどちらを非基底変数にするかを考える。上式でy = 0とすると、

λ₁= 100- x
λ₂= 100 -3x

となるが、目的関数を大きくするために、x の値を増やしていくと先にλ2 が０になってしまう（スラック変数は非負の変数であるので負になってはならない）。従って目的関数をある程度以上に大きくできないλ₂ を０にして非基底変数とする。すると、x = 100/ 3、y = 0、λ₁ =200/ 3、λ₂ =0 という新しい基底解が得られる。図ではＯからＣに移ったことになる。次にこの解がさらに改善可能かどうかを調べることにする。新しい基底変数x 、λ₁ について最初の式を解くと、

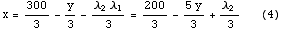
これから目的関数は

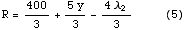
となる。ところでy は今、非基底変数としてy = 0、であるが、目的関数をみるとy　を増加させると目的関数も大きくなることがわかる。これはy　を基底変数にするとさらに解が改善されることを意味している。ところで、（４）式のy の係数は負であるから、y を増加させるとx とλ₁の両方が減少することがわかる。このどちらも負になってはならないので、y はこのどちらかが０になるところまでしか増加させられない。今、λ₂ は非基底変数なのでλ₂ = 0 として、（４）式から、x とλ₁ のそれぞれが０になる時のy を求めると、100 と40 が得られるが、先にλ₁ を０にしてしまうy = 40、までしか増加させられない。そこで（４）式を用いて、

x= 20
y= 40
λ₁= 0
λ₂= 0
(6) という新しい基底解が得られる。これは図においてＣからＢに移ったことを意味する。この時の目的関数の値は、

R=200

得られた基底解をさらに改善可能かどうかを次に調べる。（４）式からy を非基底変数λ₁ と λ₂ で表わし、目的関数の値を求めると、

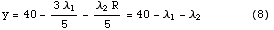
すなわち、現在の非基底変数λ₁ とλ₂ のどちらを増やしても、目的関数の値を増加させることはできない。つまり（６）が最適解である。

---

■ Mathematica による線形計画法の解法

(1)最小値問題の時は、 ConstrainedMin を使う
(2)最大値問題の時は、 ConstrainedMax を使う
(3)ベクトルや行列表現を使う場合には、LinearProgrammingを使う

---

■ 輸送問題

ある会社が資材倉庫を４ヵ所に持っている（S1,S2,S3,S4）。この資材を受入れる工場が５ヵ所あるとする（F1,F2,F3,F4,F5）。それぞれの在庫量と受入量および資材の単位あたりの輸送費が以下のように与えられている時、輸送費を最小にする問題を解く。この問題は特に輸送問題（transportation problem）と呼ばれるものである。

		工場	F1	F2	F3	F4	F5
		受入量	25	105	15	80	50
倉庫	在庫量
S1	70		25	32	48	20	84
S2	35		15	46	70	36	65
S3	110		38	52	65	27	22
S4	60		50	60	35	18	30

いま Si から Fj までの輸送資材量を x_ij,( x_ij >=0) とすると、目的関数は、
R= 25 x₁₁+ 32 x₁₂+ 48 x₁₃+ 20 x₁₄+ 84 x₁₅
+15 x₂₁+ 46 x₂₂+ 70 x₂₃+ 36 x₂₄+ 65 x₂₅
+38 x₃₁+ 52 x₃₂+ 65 x₃₃+ 27 x₃₄+ 22 x₃₅
+50 x₄₁+ 60 x₄₂+ 35 x₄₃+ 18 x₄₄+ 30 x₄₅

制約条件は、
　 x₁₁ +x₁₂ +x₁₃ +x₁₄ +x₁₅= 70
x₂₁ +x₂₂ +x₂₃ +x₂₄ +x₂₅= 35
x₃₁ +x₃₂ +x₃₃ +x₃₄ +x₃₅= 110
x₄₁ +x₄₂ +x₄₃ +x₄₄ +x₄₅= 60
x₁₁ +x₂₁ +x₃₁ +x₄₁= 25
x₁₂ +x₂₂ +x₃₂ +x₄₂= 105
x₁₃ +x₂₃ +x₃₃ +x₄₃= 15
x₁₄ +x₂₄ +x₃₄ +x₄₄= 80
x₁₅ +x₂₅ +x₃₅ +x₄₅= 50

この問題をMathematicaの関数 LinearProgramming で解く。

?LinearProgramming

LinearProgramming[c, m, b] finds the vector x which
minimizes the quantity c.x subject to the
constraints m.x >= b and x >= 0.

b={70,35,110,60,25,105,15,80,50};

m={{1,1,1,1,1, 0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0},
{0,0,0,0,0, 1,1,1,1,1, 0,0,0,0,0, 0,0,0,0,0},
{0,0,0,0,0, 0,0,0,0,0, 1,1,1,1,1, 0,0,0,0,0},
{0,0,0,0,0, 0,0,0,0,0, 0,0,0,0,0, 1,1,1,1,1},
{1,0,0,0,0, 1,0,0,0,0, 1,0,0,0,0, 1,0,0,0,0},
{0,1,0,0,0, 0,1,0,0,0, 0,1,0,0,0, 0,1,0,0,0},
{0,0,1,0,0, 0,0,1,0,0, 0,0,1,0,0, 0,0,1,0,0},
{0,0,0,1,0, 0,0,0,1,0, 0,0,0,1,0, 0,0,0,1,0},
{0,0,0,0,1, 0,0,0,0,1, 0,0,0,0,1, 0,0,0,0,1}};

c={25,32,48,20,84,
15,46,70,36,65,
38,52,65,27,22,
50,60,35,18,30};

ansv=LinearProgramming[c,m,b];

答えは、

{0, 70, 0, 0, 0,
25, 10, 0, 0, 0,
0, 25, 0, 35, 50,
0, 0, 15, 45, 0}

c.ansv

7755

輸送の総費用は、7755　である。

top

---

■ 在庫管理のシミュレーション

始めに商品の売れ方をシミュレートする関数を定義する。商品を買いに来る客が時間的にランダムに訪れるとすると、単位期間に来訪する客はポアソン分布に従う。この確率密度関数に従う乱数は、関数 Random を用いることにより得られる。

Needs["Statistics`Master`"]

平均値５のポアソン分布をもつ乱数を発生する関数を定義、

shipment:=Random[PoissonDistribution[5]];

ポアソン分布を持つ乱数をプロットしてみる。

ListPlot[Table[shipment,{30}],PlotJoined->True,
PlotStyle->RGBColor[1,0,0]];

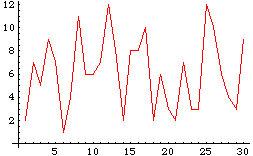
次に在庫数のシミュレーションを行う。ここで当初の在庫数をinitialStock、最低在庫数としてこれ以下になったら発注を行う数をminimumStock、発注数をstockOrder、発注してから商品が納入されるまでの期間をleadTime とする。また、商品の価格をprice、発注に関わる費用をorderCost、在庫維持のための費用stockCostを商品1個あたりの価格の10％、とすると、

orderCost = 2000 ;
price = 500;
stockCost = 0.1;
stockOrder = 300;
initialStock = 100;
minimumStock = 10;
leadTime = 4;

在庫数をシミュレートする関数を定義する。最適な発注数を調べるのが目的なので、発注数をこの関数の変数とする。

simulation[stockOrder_] :=
(totalStock = 0;
totalShipment = 0;
waiting = leadTime;
stock = initialStock;
status = {};
Table[status = Append[status, stock];
sell = shipment;
stock -= sell;
totalShipment += sell;
totalStock += stock;
If[stock <= minimumStock, ordering = "True", ordering = False];
If[ordering == "True", waiting -= 1, waiting = leadTime];
If[waiting == 0, (stock += stockOrder)];, {200}];
{stockOrder,
totalOrderCost = (stockOrder*price*stockCost/2 +
totalShipment/stockOrder*orderCost)})

関数が定義されたので、発注数を100とした場合の在庫数の変化をシミュレーションしてみる。

simulation[100];
ListPlot[status, PlotJoined -> True];

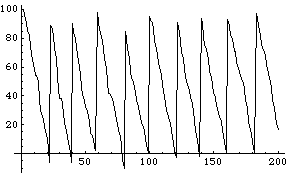
ここで、
在庫品単価：ｃ
年間総販売量：Ts
発注費用（１回あたり）：Ｋ
在庫品単位あたり維持費用（年率；％）：ｉ
１回の発注量：ｘ
在庫管理のための年間総費用：Tc

とする。年間の在庫と発注に関わる総費用は、在庫がなくなる度に発生する発注コストと在庫品の維持費用からなると考える。また、平均在庫量は、上記の在庫の変化グラフの、のこぎり状の部分が三角形であるとすれば、x/2である。すると、年間総費用は、
Tc＝Ts／x K + i c x/2
となる。そこで、上に定義された関数を用いて、発注量を変化させた時、年間総費用がどのようになるかをシミュレーションにより調べてみる。

tsc=Table[simulation[stockOrder]
,{stockOrder,100,500,50}]

{{100, 21240.}, {150, 16550.}, {200, 14870.}, {250, 14130.}, {300, 13833.3}, {350, 14521.4}, {400, 15030.}, {450, 15850.}, {500, 16552.}}

その結果をグラフにする。

ListPlot[tsc, PlotJoined -> True];

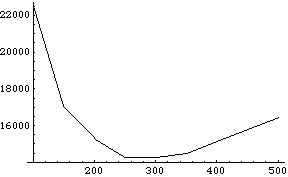
グラフから発注量300のあたりに年間総費用が最低になる点があることが予想される。

---

■ 最適発注量の公式

年間総費用は、以下のように表されるとした。
Ｔｃ＝Ts／x　Ｋ　＋　ｉ　ｃ　ｘ／２

ここで、このＴｃを最小にするような発注量を考える。発注量の変化に対するＴｃの変化量を調べるために、Ｔｃをｘで微分し、これを０とおいてｘについて解くと、最適発注量が得られる。

Tc = Ts/x K + i*c*x/2;
D[Tc, x] == 0

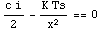
ans = Solve[D[Tc, x] == 0, x]

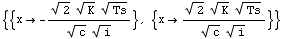
最適発注量ｘは、

Sqrt[2 orderCost* totalShipment/(stockCost *price)]

283.267

となり、シミュレーションで予想した結果が正しいことが解る。

---

■ ポアソン分布

事象が時間的にランダムに発生するとき、単位時間内に事象がｘ回発生するような確率分布のことをポアソン分布と呼ぶ。この確率分布は、待ち行列に客が到達する事象等をよく表わす。単位時間あたりの事象の平均発生回数をａとすると、その確率密度関数PDFは、以下のように表わされる。
P(x)=Exp(-a) a^x / x!ここで、x=0,1,2,.....a>0
Mathematicaで確かめてみる。

PDF[PoissonDistribution[a],x]

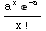
Mean[PoissonDistribution[a]]

a

確率密度関数（密度関数）をプロットしてみる。

ListPlot[Table[PDF[PoissonDistribution[0.5],x],{x,0,10}],PlotJoined->True];

---

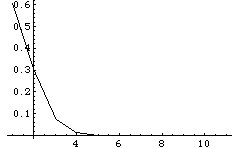
■ 指数分布

事象がランダムに発生するとき、事象の発生時間間隔は指数分布に従う。指数分布の確率密度関数は

PDF[ExponentialDistribution[lambda],x]

Exp(lambda/(lambda x)

平均時間間隔が１０単位時間である指数分布の平均値は１０である（Mean は平均を求める関数）ことが下のように確かめられる。

Mean[ExponentialDistribution[1/10]]

10

平均時間間隔が１０単位時間である指数分布に従う乱数は次のように作ることができる。

accident:=Random[ExponentialDistribution[1/10]]

そこでこの乱数を１０回発生させ、その発生間隔をプロットしてみる。

accidentList={{0,0}};t=0;
Table[t=t+accident;
accidentList=Append[accidentList,{t,0}];
accidentList=Append[accidentList,{t,1}];
accidentList=Append[accidentList,{t,0}];,{10}];
ListPlot[accidentList,PlotJoined->True];

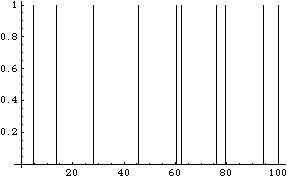
課題

それでは、上の図が平均時間間隔が１０年であると考えられる事故を表わしていると考えた時、飛行機事故の場合によく言われるように大事故は続けて起きる、という言説はどのように説明するべきであろうか。また上のシミュレーション結果と直感的な予想との間にずれがないだろうか。シミュレーションのプロット結果とともに、論ぜよ。

top

待ち行列とは、あるサービスを提供する窓口に、客などサービスを必要とする人、物等が次々と到着して、サービスが間に合わないときに、窓口にできる行列のことである。このようにサービス提供能力が不足して待ち行列が長くなると、サービスを受けられない客は他に逃げていってしまうであろうから、利益機会の損失と客の信用損失を招いてしまう。

一方、待ち行列を解消しようとして窓口を増やすと、客などの到着が少ない場合に、窓口が遊んでいる状態（遊休状態）が生じ、遊休状態の窓口を維持する余分な費用が必要となる。問題は、このどちらの状態になっても、余分な費用が発生することである。待ち行列の問題とは、この相反する費用の合計をいかに小さくするかの解を与えることである。

この待ち行列の問題を最初に扱ったのはアーラン（A.K.Erlang）である。アーランはデンマークの電話会社技師で１９００年代に初めて待ち行列問題を数学的に取り扱った。現在も、電話等回線のトラフィック量（回線が呼で保留されている延べ時間）を表わす単位としてアーラン（erl）が用いられる。

---

待ち行列の例、バス待ち合わせの問題

バスが正確に１０分間隔で運行されているとする。ランダムにバス停にやってくる客が平均してバスを待つ時間を考える。簡単のため、１分単位で事象を表わすとすると、客の待つ時間の期待値E(Tw)= 0.1*0　+0.1*1　+0.1*2　+... +0.1*9 =　4.5分である。0.5分単位で同じことを考えると、客の待つ時間の期待値E(Tw)= 0.05*0　+0.05*0.5　+0.05*1　+... +0.05*9.5 =　4.75分となる。 これを0.25分単位で考え、その期待値を計算すると、

n = 0.25;
Sum[n/10* n *(i - 1), {i, 1, 10/n}] // N

4.875

となる。そこでこの事象を考える単位を0にまで短くしてみると、

Limit[Sum[m/10* m *(i - 1), {i, 1, 10/m}], m -> 0]

5

得られた5分という結果は、常識的に納得できる。さて、実際にバスを待った経験から言えば、5分より長い感覚を持っていないだろうか。いま、平均的にはT 分間隔でバスが運行されているとき、１分単位で事象を表わすとすると、客がバス停に来てから、１分遅れてバスが到着する確率は1/T である。２分遅れてくる確率は、最初の１分にバスがこない確率(1-1/T) に次の１分に到着する確率をかけて、
(1-1/T)*1/T と表わされる。３分遅れる確率は、(1-1/T)^2*1/T となる。従って、客の待つ時間の期待値は、
E(Tw)= 1*1/T +2*(1-1/T)*1/T+3*(1-1/T)^2*1/T ... =T である。

上式の総和を求めると、

Sum[n (1/T)(1-1/T)^(n-1),{n,1,Infinity}]

T

つまり、平均的に10分間隔で運行されているバスの待ち時間の期待値は10分である。実際には、正確に10分間隔に運行される場合と平均的に10分間隔で運行される場合の中間であろうから、客は5分より長く10分より短い時間の間、バスを待たねばならないであろう。

---

待ち行列のシミュレーション

始めに統計パッケージを読み込む。

Needs["Statistics`Master`"]

次に、客の到着時間とサービス時間を定義する。客はポアソン到着し、指数サービスを受ける。窓口は一つとする。

客がポアソン分布に従って到着することをポアソン到着という。到着を表わすのに、平均到着率λ（平均到着時間間隔の逆数）がよく使われる。サービス時間が指数分布に従うとき、これを指数サービスという。サービスを表わすのに、平均サービス率μ（平均サービス時間の逆数）がよく使われる。

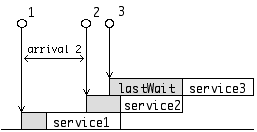
arrivalMean=10;
serviceMean=6;
nPerson=100;

lambda=1/arrivalMean;
myu=1/serviceMean;
arrival:=Random[ExponentialDistribution[lambda]];
service:=Random[ExponentialDistribution[myu]];

シミュレーションを行う関数 simRun を定義する。

simRun:=(
lastWait=0;
waiting=0;
totalWait=0;
waitList={{0,0}};
Table[
lastService=service;
myArrival=arrival;
If[lastService+lastWait>myArrival,
(* if True, increment of the waiting *)
waiting+=1;
lastWait=lastService+lastWait-myArrival,
(* if False, decrement of the waiting *)
waiting=Max[waiting-=1,0];
lastWait=0];
totalWait+=lastWait;
waitList=Append[waitList,{totalWait,waiting}],
{i,nPerson}];
totalWait/nPerson)

上記で定義した関数を実行してみる。

simRun

13.4841

上の数字がシミュレーションによる、客の平均待ち時間である。

客がサービスを受けるまでの平均待ち時間は、待ち行列が定常的になった場合に、以下の式で与えられる。

lambda/(myu(myu-lambda))

客が待ち行列に並ぶ様子を横軸に時間、縦軸に行列している人数をとってプロットしてみる。

ListPlot[waitList,PlotJoined->True];

---

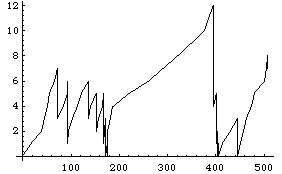
課題

上記のシミュレーションのパラメータ、arrivalMean,serviceMean,nPersonに任意の数値を与えて、シミュレーションを１０ないし２０回繰り返し、客の平均待ち時間がどのようになるかを調べよ。また、その結果をlambda/(myu(myu-lambda)) で計算される値と比較せよ。両者に違いのある場合、それはなぜか。

上で定義した関数、simRun を好きなだけ繰り返し計算するプログラムを　関数　Table[] を使って書き、関数 Mean[] を使って平均を求めると便利である。

top

ゲームの理論の目的は、理論の現実への応用ではなく、この理論を通してものごとをよりはっきりと見ることができるようにすることである。ゲームの理論のみならず、こうした形式的なモデルがあった方がモデルなしでものごとを見るよりも、ものごとを動かす本質をはっきり捉えることができる。−Robert Axelrod

---

二者ゼロ和（zero sum)ゲーム

二人もしくは二つの組織が競争している時、一方の利益が他方の不利益となる場合がある。このような競合問題に関する理論がゲームの理論である。ゲームの理論では、このような競合状態をゲームと呼ぶ。ゲームの終了時に一方の得る価値が他方の失った価値と等しい場合、これを二者ゼロ和（zero sum)ゲームと呼び、それ以外を非ゼロ和ゲームと呼ぶ。二者ゼロ和ゲームについては、ゲーム理論を開発したVon.Neumann により理論的に解明されている。

---

純粋ゲーム

今、青軍（Brue）と赤軍（Red）が戦っているとする。青軍は前線の味方に物資を補給しようとしている。これに対し、赤軍は途中でこれに待ち伏せ攻撃を加え、青軍の物資補給を妨害しようとしている。この時、青軍が選ぶ可能性のある補給路は r１、r２、３の三つがあり、赤軍が始めに攻撃することにした補給路 r１、r２、３のそれぞれの場合について実際に攻撃できる日数が、以下の表のようになっているとする。例えば、赤軍は、青軍が補給路r１をとると仮定して、これを最初から攻撃できれば、攻撃日数として９日が得られるので最大の成果をあげられるはずである。しかし、青軍が裏をかいてr２を補給路として選ぶと、赤軍は攻撃方面を変更しなけれならず、たった１日の攻撃日数しか与えられないことを示している。

		青軍の物資補給路
		r1	r2	r3
赤軍の攻撃路	r1	8	1	2
	r2	3	7	4
	r3	7	6	5

この例では、赤軍は攻撃できる日数を最大にしたいと考えるし、青軍は攻撃される日数を最小にしたいと考える。問題は互いに相手がどの補給路を目指すかが不明な点にある。

この問題を赤軍は次のように解決する。まず青軍は赤軍の動きを何らかの方法で予知することが可能で、また、その予知に対して合理的な対応を行うものと考える。すると、赤軍がr１を攻撃するとすれば青軍は攻撃日数を最小の１日にするr２を選ぶであろう。赤軍がr２を攻撃するとすれば、青軍はr１を選んで攻撃される日数を３日とするであろう。また、赤軍がr３を攻撃するとすれば、青軍はr３を選んで攻撃される日数を最小の５日とするであろう。とすれば、赤軍は青軍が選んだ最小の日数である、１日、３日、５日のうち、攻撃日数が最大となるr３を選ぶべきである。

一方、青軍は次のように考える。やはり赤軍は青軍の動きをなんらかの方法で予知が可能で、予知結果に対して合理的な対応を行うものと考える。青軍がr１を補給路に選べば、赤軍は攻撃日数を最大の８日にするr１を選ぶであろう。青軍がr２を補給路に選べば、赤軍は最大７日の攻撃日数をとれるr２を選ぶであろう。また、青軍がr３を選べば赤軍は最大５日の攻撃日数をとれるr３を選ぶであろう。とすれば、青軍としては、赤軍の選ぶであろう最大の攻撃日数である、８日、７日、５日のうち、攻撃される日数の最小となるr３を選ぶべきである。

上記の結果から、赤軍はr３を攻撃するのが最も有利である。この結論に至る手法をミニマックス戦略（minimax strategy）という。これは青軍からみるとマキシミン（maxmin strategy）戦略と言う。

赤軍の利益は攻撃日数で表わされるが、逆に青軍の不利益は攻撃される日数で、両者の利益と不利益を加えると０となるので、上の例は二者ゼロ和ゲームである。この例ではそれぞれの利益を日数で表わしたが、一般的にはこの利益を、支払われる利益という観点から見ることにして、このゲームの参加者の戦略の組み合わせによる支払いの表をペイオフ・マトリックス(Pay-off （完済）matrix ）と言う。またペイオフ・マトリックスは、支払いを最大化する方を基準として作る。また、一方のミニマックス戦略により得られた値と、他方のマキシミン戦略によって得られた値はそれぞれにとってのゲームの値である。ゲームの値が一致するとき、このようなペイオフ・マトリックスは鞍点（saddle point）を持つという。鞍点を持つゲームのことを純粋ゲーム、その戦略を純粋戦略と呼ぶ。また、上記の例では、赤軍と青軍の選び得る戦術は３種類であるとした。このように選び得る戦術（手）が有限であるとき、このゲームを有限ゲームと呼ぶ。

Plot3D[x^2-y^2 , {x,-1,1},{y,-1,1},Axes -> None];

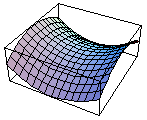
鞍点の例

---

混合戦略ゲーム

次のようなペイオフ・マトリックスを持つ二者ゼロ和ゲームを考える。ここでは、ペイオフ・マトリックスが赤の利益を最大にする立場で作られているとする（青のペイオフ・マトリックスは、この表の値に負号をつけたものに等しいとする）。

		青の攻撃方法
		G	C	P
赤の攻撃方法	G	1	2	0
	C	0	1	2
	P	2	0	1

赤のミニマックス戦略を考えると、赤のゲームの値は０となる。一方、青のマキシミン戦略から青のゲームの値は２である。両者のゲームの値は一致しない、つまりこのゲームは鞍点を持たない。このような場合、赤の攻撃と青の要撃が繰り返し行われるとして両者の手段がある割合で選ばれ、その組み合わせの結果によりゲームの様子を調べる、という方法をとる。このようなゲームを混合戦略ゲームと呼ぶ。

---

有限ゼロ和ゲームの線形計画法による解法

有限ゼロ和ゲームは線形計画法により解くことができる。上記の例で赤がG、C、Pの攻撃方法をそれぞれx１、x２、x３の確率で選択するものとする。このとき、期待できる利益がvであるとすれば、青がGの要撃方法をとる場合、C、Pの場合のそれぞれを考えて、

x1+ 2 x3 >=v
　 2 x1+ x2 >=v
2 x2+ x3>=v
x１、x２、x３の戦術の確率を合わせると１だから、

x1+ x2+x3=1
ここで、x１、x２、x３をそれぞれ x１＝x１／v、 x２＝x２／v、 x３＝x３／v　と置き換えると、上の問題は、
x1+ 2 x3 >=1
　 2 x1+ x2 >=1
2 x2+ x3>=1
の条件の時、x1+ x2+x3=1／v　を最小にするx１、x２、x３を求める問題になる。

ConstrainedMin[ x1+x2+x3,
{x1+2 x3>=1,
2 x1+ x2>=1,
2 x2+ x3>=1}, {x1,x2,x3}]

{1, {x1 -> 1/3, x2 -> 1/3, x3 -> 1/3}}

この問題の結果は、G、C、Pの手をそれぞれ１／３の確率で用いれば、期待される利益が最大化され、その値は１であることを示している。

---

二者非ゼロ和ゲーム

既に理論的にも解明されている二者ゼロ和ゲームに対して、二者非ゼロ和およびゲームの参加者が３人以上の数の非ゼロ和ゲームは研究の途上にある。

---

代表的二者非ゼロ和ゲーム〜囚人のジレンマ

囚人のジレンマとは以下の様なゲームである。ある事件で共謀した犯人が二人つかまっている。二人は別々の独房に入れられており、取り調べに対して黙秘か自白かの二つの方法がある。二人が共に黙秘すればこの事件の証拠は不十分となり刑は余罪の分だけで２年ですむ。二人とも自白すれば事件が立証されるが、自白したことを考慮して二人とも４年の刑になる。しかし一方が自白し、一方が黙秘した場合、黙秘した方は５年の刑で自白した方は無罪放免となるとする。一般にゲームから得られる利得や満足を表にしたものを利得マトリックスと呼ぶ。この時の二人の利得マトリックスは次のようになる。

		B
		自白	黙秘
A	自白	-4,-4	0,-5
	黙秘	-5,0	-2,-2

例えばＡが自白し、Ｂが黙秘したとする。この時のＡとＢの利得は表の右上に表わされており、それぞれ０と−５である。二人の囚人の利得は加え合わせても０にならない。それぞれの囚人はどのような方法を選ぶであろうか。Ａについての利得マトリックスを作ってみると、以下のようになる。

		B
		自白	黙秘
A	自白	-4	0
	黙秘	-5	-2

既に述べたようにこれは線形計画法により解くことができる。線形計画法で計算するために、便宜上、表の値に５を加えることにする。

		B
		自白	黙秘
A	自白	1	5
	黙秘	0	3

Ａが自白する割合をx１、黙秘する割合をx２とすると、　　

ConstrainedMin[ x1+x2,
{x1 >=1,
5 x1 +3 x2>=1}, {x1,x2}]

{1, {x1 -> 1, x2 -> 0}}

結果としてＡは自白する。ＢについてもＡと同じ条件であるので自白することになる。両者が黙秘すれば、お互いに最も高い利得が得られるのに、互いが合理的判断をするという仮定に立つと低い利得しか得られない。これが囚人のジレンマである。

---

囚人のジレンマからの脱出

囚人のジレンマは社会のいろいろな局面で出現していると考えられる。囚人のジレンマの利得マトリックスに５を加えて次のような新たな利得マトリックスを作って見る。この例は例えば、学生サークルの部屋の掃除をＡとＢがすることになっている状況と考えることができる。

		B
		裏切り	協力
A	裏切り	1, 1	5, 0
	協力	0, 5	3, 3

囚人のジレンマは１回しか出現しないであろうが、この場合、ジレンマに何度も遭遇することになる。そこで三つの戦略を考えてみる。
（ａ）でたらめ戦略：　　等しい確率で裏切りか協力かを選ぶ。
（ｂ）裏切り戦略：　　　常に裏切る。
（ｃ）しっぺ返し戦略：　協力を基本とするが、相手が裏切ったら次回にこちらも裏切る。

最初に Mathematicaで各戦略を定義する。

strategyA[]:=If[Random[Integer,{0,1}]==0,betrayal,cooperation];
strategyB[]:=betrayal;
strategyC[]:=lastMatch;

次にａとｂに各々、戦略を与えてこれを１００回、対戦させるシミュレーションを行う。

markA=markB=0;
lastMatch=cooperation;
Table[{a=strategyA[];
b=strategyC[];
If[a==betrayal && b==betrayal, {markA+=1,markB+=1}];
If[a==betrayal && b==cooperation, {markA+=5,markB+=0}];
If[a==cooperation && b==betrayal,{markA+=0,markB+=5}];
If[a==cooperation && b==cooperation,{markA+=3,markB+=3}];
lastMatch=a;},{i,100}];

シミュレーションした結果の得点を調べる。

{markA,markB}

{236, 231}

---

課題

以下の表の空欄を埋めること。

	でたらめ戦略	裏切り戦略	しっぺ返し戦略	総得点
でたらめ戦略
裏切り戦略
しっぺ返し戦略

戦略を変えてシミュレーションを行う場合は、
a=strategyA[];
b=strategyC[];
の部分を変えるとよい。
b=strategyC[];の時は、lastMatch=a;（ｂから見た場合、ａの直前の手）、
a=strategyC[];の時は、lastMatch=b;（ａから見た場合、ｂの直前の手）とすることに注意。

---

参考文献

勝つためのゲームの理論、西山賢一、講談社ブルーバックス
ゲームの理論入門、モートン・D・デービス、講談社ブルーバックス
ＯＲ入門、日経文庫、宮川公男
オペレーションズ・リサーチ／理論と実際、培風館、佐治信男　他
パソコンによるＯＲ、朝倉書店、牧野都治・牧野京子
MathematicaによるOR (Higher Education Computer Series) 、中村 健蔵
囚人のジレンマ、青土社、ウィリアム・パウンドストーン・松浦俊輔　訳
失敗の本質、中公文庫、戸部良一　他
アメリカ海兵隊、中公新書、野中郁次郎
大本営参謀の情報戦記、文春文庫、堀栄三
ＰＥＲＴの知識、日経文庫、加藤昭吉
組織科学の話、日経文庫、山田雄一

top